In part 2 I showed how we can work out the 'best' aperture for macro photography based on the following variables:
- The optical magnification (m)
- The pupil magnification (p)
- The acceptable total circle of confusion (c)
- A factor, k, to account for the post production impact of the diffraction, ie 0 means ignore diffraction, 0.5 assume a 'weakish' impact and 1 assume the 'full' Airy impact.
I also showed how you can find the pupil magnification through the PhotonsToPhotos optical bench hub. Of course if your lens is not in the list of lenses, you will need to measure or guess the pupil magnification yourself.
As many macro photographers will be using a lens set to a specific optical magnification, there is no need to worry knowing the focus distance, as we do in non-macro photography. We thus 'only' need to solve the following to arrive at an estimate of the total depth of field (d) in mm; where m, p, c and k are the four variables that you need to know to match your camera/lens settings and presentation needs:
Note that c in the above is in mm, with the other input terms being dimensionless.
As some will look at the above and be intimidated by the maths, here is a link to a WolframAlpha page (no need to supply any personal details) that allows you to input your m, p, k and c values on the input line at the top of the WolframAlpha screen; with WolframAlpha doing the maths for you to solve for d and, on the way, highlight the optimum aperture (N). Note that you need to select approximate in the Solution box to get a decimal output, also use a small k value to switch off diffraction, say 0.1, else you will get a ‘no solution’ result.
As an example, lets take a Canon 100mm macro lens and use the PhotonsToPhotos Hub to find the pupil magnification at an optical magnification of 1. Note the aperture of F/10 is arbitrary, ie the pupil magnification does not change with aperture:
Here we see that at a magnification of 1, the lens has a pupil magnification of 0.28. Let's assume a circle of confusion of 0.03mm, ie 30 microns, and that we can use our software tools to recover some of the diffraction softening, thus we will use a 'weak diffraction model' and a k value of 0.5.
Plugging the above into the WolframAlpha link gives the following:
Here we see that, if shooting with the Canon 100mm macro at unity magnification, we will maximise the diffraction aware depth of field by shooting at F/6.5, which will result in a total depth of field of about 1.3mm, ie about 0.65mm either side of the plane of focus.
The above is all useful information if we are focus stacking with a rail (more on this in a future post).
If handholding, single shooting or attempting to focus bracket by moving the camera's position relative to the subject, this depth of field is very challenging, unless you are Thomas Shahan, say :-)
However, we have a few things that can help those of us that need it.
First, modern sensors tend to have a good resolution, thus, although a magnification of 1 is great, we could get away with a magnification of, say, 0.5, ie about half the linear resolution on the object, relative to unity magnification.
Second, we have software that purports to 'recover' the image quality by 'AI algorithms', for example the new Adobe Enhance feature.
Based on this, let's now look at backing the optical magnification off to, say, 0.5; which results in the following lens characteristics:
Here we see that the pupil magnification has now changed to 0.58, resulting in the following DoF estimate:
That is our diffraction aware depth of field is now estimated to be about 5.3mm, shooting at F/16. Although the object will take up about a quarter of the sensor area of the previous set up, with a modern sensor this should be OK: as long as we are not seeking to create too large a print and the exposure is still ok.
I hope this addendum has helped some, and, as usual, I welcome any feedback on this post or any of my posts.
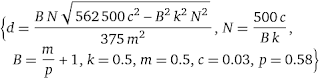




No comments:
Post a Comment